Graphs

Java Chapter 18 - Graphs

18.1 Graphs

A graph is a data structure that can be used for finding paths shortest paths in real world problems. A graph consists of vertices (nodes) and edges (lines).

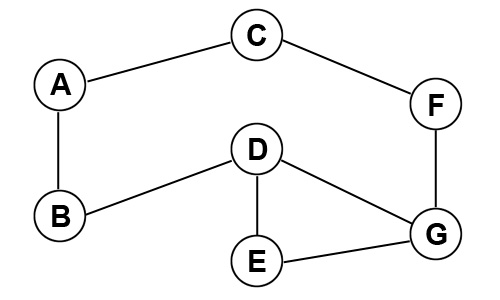
1. Undirected Graph - The graph below has vertices 7 vertices (A - G) and 8 edges connecting them. There are 3 different paths to travel from A to G.

2. Directed Graph - This graph has directed edges that allow you to only travel between vertices in the direction of the arrow. There is only 1 path to travel from A to G - (A:B), (B:E), (E:G)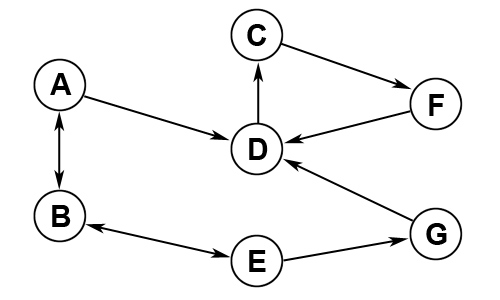
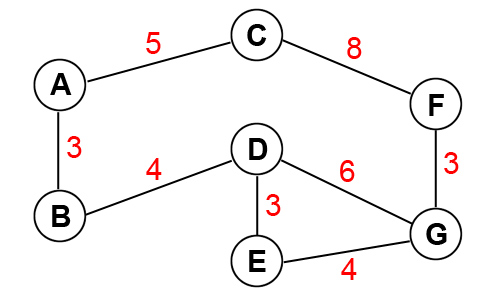
3. Weighted Graph - This graph has a weight for each edge. This could be used for calculating distances between objects. Using the weights, we see the shortest path from A to G is 13 - (A:B), (B:D), (D:G)

18.2 Dijkstra's Shortest Path

In graph theory, the shortest path problem is finding the best path between two vertices after considering the weights of the edges. There are many algorithms that work with different types of graphs. Below is an implementation of Dijkstra's algorithm using a graph of castle room objects as first discussed in chapter 15. The vertices (rooms) are stored in an array called Vertex.

class Room
{
    String RoomName;
    Room North, South, East, West;

    boolean Visited;   // used for Dijkstra
    int Distance;      // used for Dijkstra

    Room (String theRoomName)
    { RoomName = theRoomName; }
}

// Dijkstra's Shortest Path
static int ShortestPath(Room Start, Room Finish)
{
	for (int i=0; i<Vertex.size(); i++)
	{
		if (Vertex.get(i) == Start)
			Vertex.get(i).Distance = 0;
		else
			Vertex.get(i).Distance = 1000;  // set distance to "infinity"
		Vertex.get(i).Visited = false;
	}

	Room Temp = Start;
	while (!Finish.Visited)
	{
		Temp.Visited = true;
		if (Temp.North!=null && !Temp.North.Visited && Temp.North.Distance > Temp.Distance+1)
			Temp.North.Distance = 1 + Temp.Distance;
		if (Temp.South!=null && !Temp.South.Visited && Temp.South.Distance > Temp.Distance+1)
			Temp.South.Distance = 1 + Temp.Distance;
		if (Temp.East!=null && !Temp.East.Visited && Temp.East.Distance > Temp.Distance+1)
			Temp.East.Distance = 1 + Temp.Distance;
		if (Temp.West!=null && !Temp.West.Visited && Temp.West.Distance > Temp.Distance+1)
			Temp.West.Distance = 1 + Temp.Distance;

		int Smallest = 1000;
		int SmallestIndex = -1;
		for (int i=0; i<Vertex.size(); i++)
		{
			if (!Vertex.get(i).Visited && Vertex.get(i).Distance < Smallest)
			{
				Smallest = Vertex.get(i).Distance;
				SmallestIndex = i;
			}
		}
		Temp = Vertex.get(SmallestIndex);
	}
	return Finish.Distance;
}

18.3 JGraphT Library

JGraphT is a free Java Graph library. It will need to be downloaded and added to your compiler's class path:

- TextPad: Go to Configure, Preferences, Environment Variables. Add a path to your jar to the CLASSPATH:
C:\java\jgrapht-0.9.0\lib\jgrapht-core-0.9.0.jar;%CLASSPATH%

- Eclipse: Go to the properties of your project, select Java Build Path, Libraries tab, and Add JAR.

Below are some of the methods in the graph library.

Creating a Graph	Description
DirectedGraph<String, DefaultEdge> g = new DefaultDirectedGraph<String, DefaultEdge> (DefaultEdge.class);	Create a directed graph of Strings named g
SimpleWeightedGraph<String, DefaultWeightedEdge> g = new SimpleWeightedGraph<String, DefaultWeightedEdge> (DefaultWeightedEdge.class);	Create a weighted graph of Strings named g
Methods	Description
g.addVertex("Dallas");	Adds a vertex named Dallas
g.containsVertex("Dallas");	Returns true if Dallas exists
g.addEdge("Dallas","Austin");	Adds an edge to the graph
g.setEdgeWeight(g.getEdge("Dallas","Austin"),200);	Set edge weight between Dallas and Austin to 200
g.edgesOf("Dallas")	Returns a set of edges touching Dallas
g.vertexSet()	Returns a list of all vertices
g.vertexSet().size()	Returns the number of vertices
g.edgeSet()	Returns a list of all edges
g.edgeSet().size()	Returns the number edges
g.getEdgeWeight(g.getEdge("Dallas","Austin"))	Returns the edge weight from Dallas to Austin
g.removeVertex("Dallas")	Removes vertex Dallas
g.removeEdge(g.getEdge("Dallas","Austin"))	Removes the edge from Dallas to Austin

The program below creates a directed graph, adds 3 vertices, and 5 edges. It then finds the shorted path from v3 to v1.

graph_directed.java

import java.util.*;
import org.jgrapht.*;
import org.jgrapht.graph.*;
import org.jgrapht.alg.*;

public class graph_directed
{
    public static void main (String[] args)
    {
        DirectedGraph<String, DefaultEdge> g =
        new DefaultDirectedGraph<String, DefaultEdge>(DefaultEdge.class);

        g.addVertex("v1");
        g.addVertex("v2");
        g.addVertex("v3");
        g.addEdge("v1","v2");
        g.addEdge("v2","v3");
        g.addEdge("v3","v2");
        g.addEdge("v2","v1");
        System.out.println(DijkstraShortestPath.findPathBetween(g, "v3", "v1"));
    }
}

Output

The program below creates a weighted undirected graph, adds 3 vertices, adds 3 edges, and sets the weights of the 3 edges. It then calculates the shortest path and length.

graph_weighted.java

import java.util.*;
import org.jgrapht.*;
import org.jgrapht.graph.*;
import org.jgrapht.alg.*;

public class graph_weighted
{
    public static void main (String[] args)
    {
        SimpleWeightedGraph<String, DefaultWeightedEdge> g =
        new SimpleWeightedGraph<String, DefaultWeightedEdge>(DefaultWeightedEdge.class);

        g.addVertex("A");
        g.addVertex("B");
        g.addVertex("C");
        g.addEdge("A","C");
        g.addEdge("A","B");
        g.addEdge("B","C");
        g.setEdgeWeight(g.getEdge("A","C"),50);
        g.setEdgeWeight(g.getEdge("B","C"),20);
        g.setEdgeWeight(g.getEdge("A","B"),20);

        DijkstraShortestPath path = new DijkstraShortestPath<>(g, "A", "C");
        System.out.println("Path = " + path.getPathEdgeList());
        System.out.println("Length = " + path.getPathLength());
    }
}

Output