
The numbering system we use for most purposes is called the Decimal. It consists of 10 numbers: 0123456789.
In the past, some civilizations used other numbering systems. For example, the Babylonians used the sexagesimal system, based on the number 60.
This numbering system is why there are 60 minutes in an hour and 360 degrees (a multiple of 60) in a circle.

The Mayas used the vigesimal system, based on the number 20.

A base-1 numbering system was used by some people in ancient times before more advanced systems were developed. In a base-1 system, you simply put a tally mark (or a 1) for each item you are counting. For example, this ancient stick has 29 notches, possibly corresponding to the cycle of the moon:

Tally marks is
another example of the unary numbering system.

A numbering system that has elements of both Unary and Decimal is Roman - I, V,
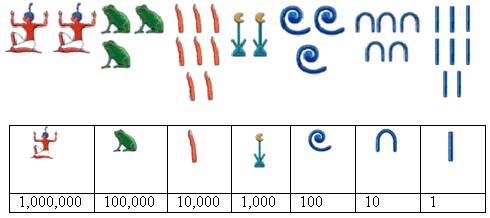
X, L, C, D, M. The ancient Egyptian numbering system is similar. The number below is 2,382,358.
The electronic circuitry within computers is composed of switches (latches) that have two states - on and off. Programmers represent the "on" state as 1 and the "off" state as 0. Since each switch has two states, the binary numbering system was created.
You may have noticed the 1 and 0 on power switches representing on and off.

Counting in binary can be tricky at first. The table below shows that you can count to 15 with a 4-digit binary number.
| 4-Digit Binary | Decimal | 4-Digit Binary | Decimal |
| 0000 | 0 | 1000 | 8 |
| 0001 | 1 | 1001 | 9 |
| 0010 | 2 | 1010 | 10 |
| 0011 | 3 | 1011 | 11 |
| 0100 | 4 | 1100 | 12 |
| 0101 | 5 | 1101 | 13 |
| 0110 | 6 | 1110 | 14 |
| 0111 | 7 | 1111 | 15 |
| Binary Number | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| Value of Each Digit | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Add the values in which the binary is a one: 128 + 32 + 16 + 4 + 1 = 181
A bit is a single binary digit, which can be 1 or 0. A byte is 8 binary digits (8 bits), which allows you to count from 0 to 255. Data in computers is organized in bytes. The following table shows how the metric system is used to represent bytes.
| Unit | Size | What it Can Store |
| bit | 1 or 0 | One bit can store answers to true/false or yes/no questions. E.g. Are you Covid-19 vaccinated? |
| byte | 8 bits | A byte can store a number from 0 - 255. Each character of an ASCII document can be stored using one byte. |
| kilobyte (KB) | 1,000 bytes | A kilobyte can store a page of text. Note: Sometimes a kilobyte is shown as 1,024 because it is a multiple of 2. |
| megabyte (MB) | 1,000,000 (million) bytes | A megabyte can store the text in a book. |
| gigabyte (GB) | 1,000,000,000 (billion) bytes | 6 GB can store an HD movie. 100 gigabytes can store a 4K movie. |
| terabyte (TB) | 1,000,000,000,000 (trillion) bytes | 10 TB can store the printed section of the Library of Congress. |
| petabyte (PB) | 1015 (quadrillion) bytes | Is is estimated that the human brain can store 2.5 PB of data. |
| exabyte (EB) | 1018 (quintillion) bytes | The size of data centers such as Google, Facebook, and AWS is measured in exabytes. |
| zettabyte(ZB) | 1021 (hextillion) bytes | The size of the entire World Wide Web is measured in zettabytes. |
| yottabyte (YB) | 1018 (septillion) bytes | A yottabye can store all of Yoda's knowledge ;-) |
Example 1: You have some video files that are 2 GB each. How many of these files will fit on a 1 TB external hard drive?
Solution:
1
TB 1,000,000,000,000 1,000
---- = ----------------- = ----- =
500 video
files
2 GB 2,000,000,000 2
Example 2: How many 8 MB photos will fit on a phone with 24 GB free space?
Solution:
24
GB 24,000,000,000 24,000
----- = -------------- = ------ =
3000 photos
8 MB 8,000,000 8
Hexadecimal is used by programmers to be a human-friendly representation of binary. It replaces 4 binary digits (bits) with one hex digit. Therefore, two hex digits are used to represent a byte. The table below shows 4 bits and the hex equivalent.
| 4-Digit Binary | Dec | Hex | 4-Digit Binary | Dec | Hex |
| 0000 | 0 | 0 | 1000 | 8 | 8 |
| 0001 | 1 | 1 | 1001 | 9 | 9 |
| 0010 | 2 | 2 | 1010 | 10 | A |
| 0011 | 3 | 3 | 1011 | 11 | B |
| 0100 | 4 | 4 | 1100 | 12 | C |
| 0101 | 5 | 5 | 1101 | 13 | D |
| 0110 | 6 | 6 | 1110 | 14 | E |
| 0111 | 7 | 7 | 1111 | 15 | F |
Often, a hexadecimal number is written with a 0x in front of it: 0xB means B hex, or 11 in decimal. OxFF means FF hex, or 255 in decimal.
Since computers only store numbers, they need a coding system to represent text. One popular coding system used by Windows computers is ASCII. Each character of text is stored using one byte (8 bits) of memory. Spaces (ASCII 32) and punctuation marks also use one byte. Therefore, this sentence takes 40 bytes.
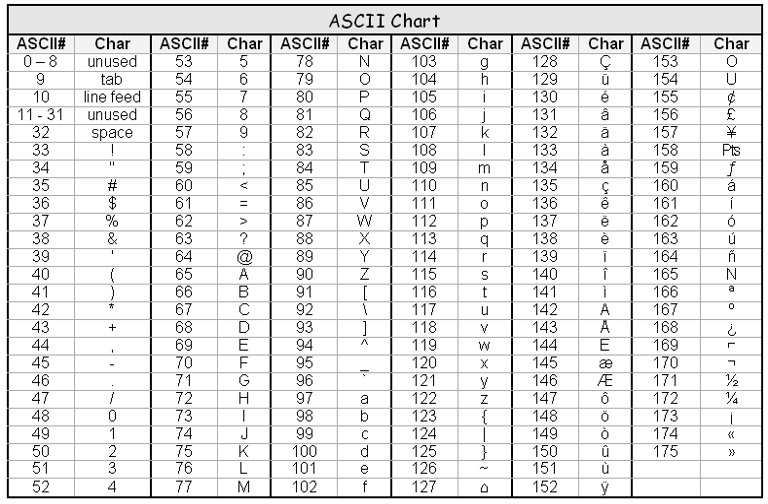
The extended ASCII characters (above 127) do not have keys on the keyboard. On Windows, these can be recreated by holding the Alt key and typing the ASCII number on the keypad (assuming you have a full keyboard). For example, hold the Alt key and type "171" on the keypad for the character ½.